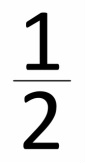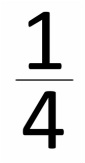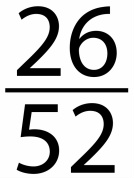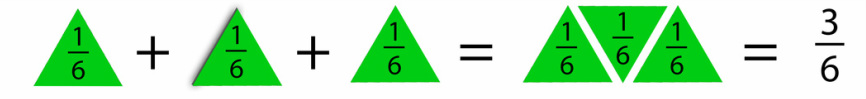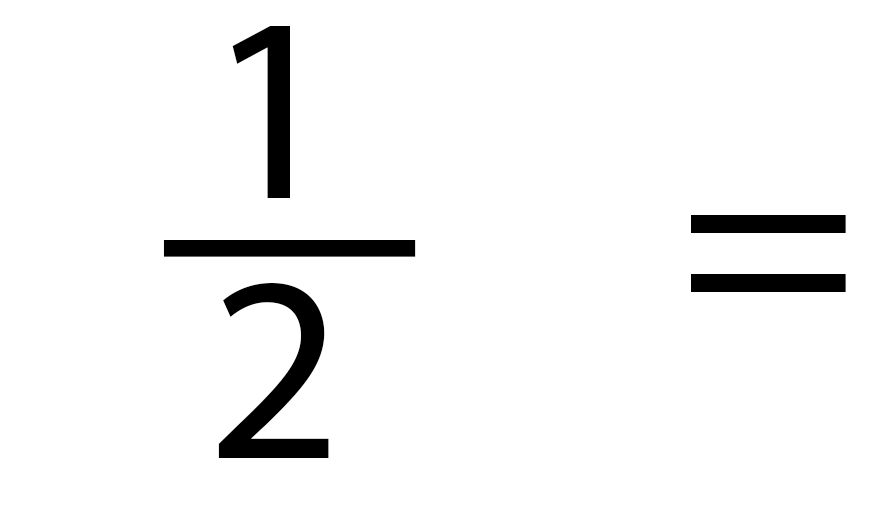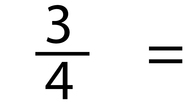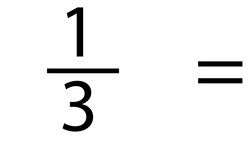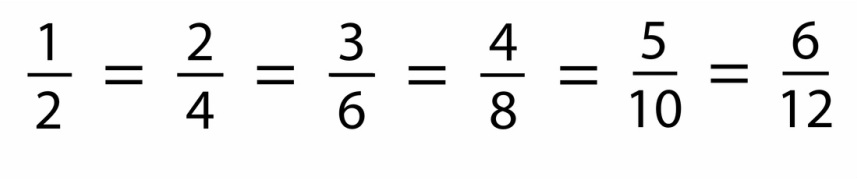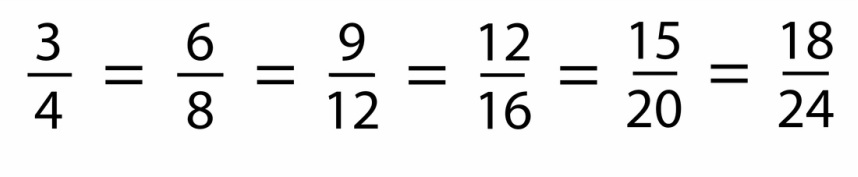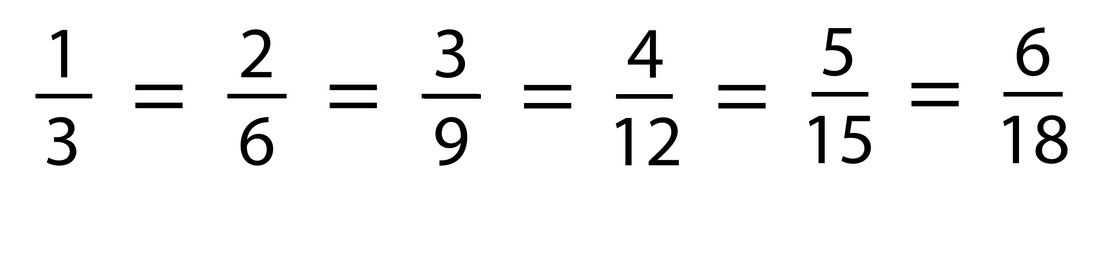fractions and their uses, chance and probability
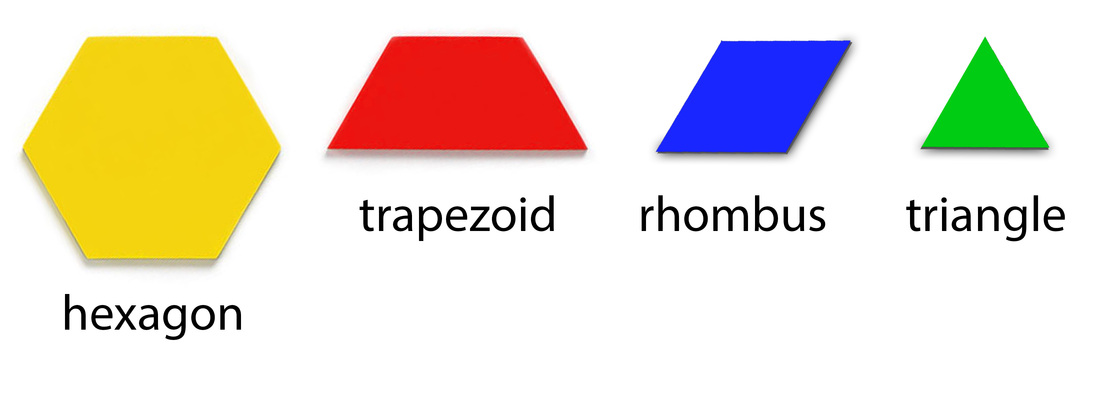
7.1 Basic Fraction Concepts
|
|
|
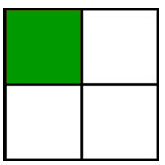
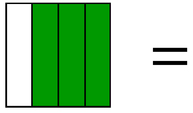
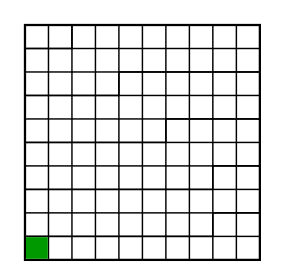
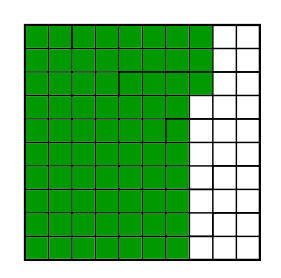
A fraction is always a part of something - for example...
The something is called the whole or ONE. When measuring we call the whole the unit.
|
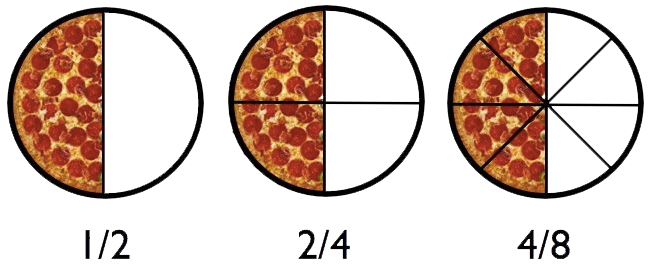
For example, Mr. C came home from school and was really hungry. He decided to make a pepperoni pizza. He rolled out the dough, added the sauce, cheese, and pepperoni. After it had baked in the oven, he cut the pizza into 4 equal parts and ate one slice for dinner. If Mr. C has 3/4 of a pizza left, the pizza is the "whole." The fraction 3/4 tells us that the pizza was divided into four equal parts. It also tells us that Mr. C has 3 pieces left. |
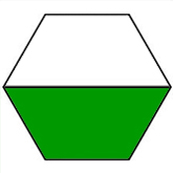
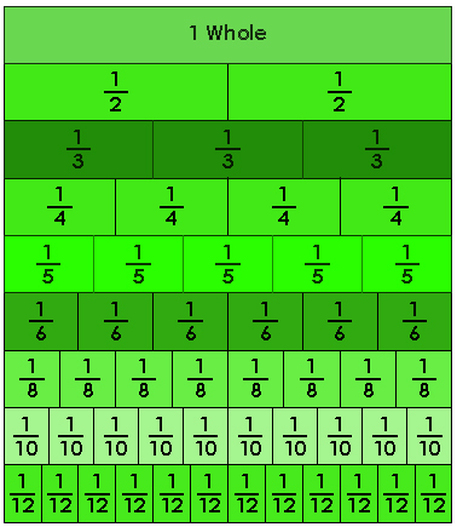
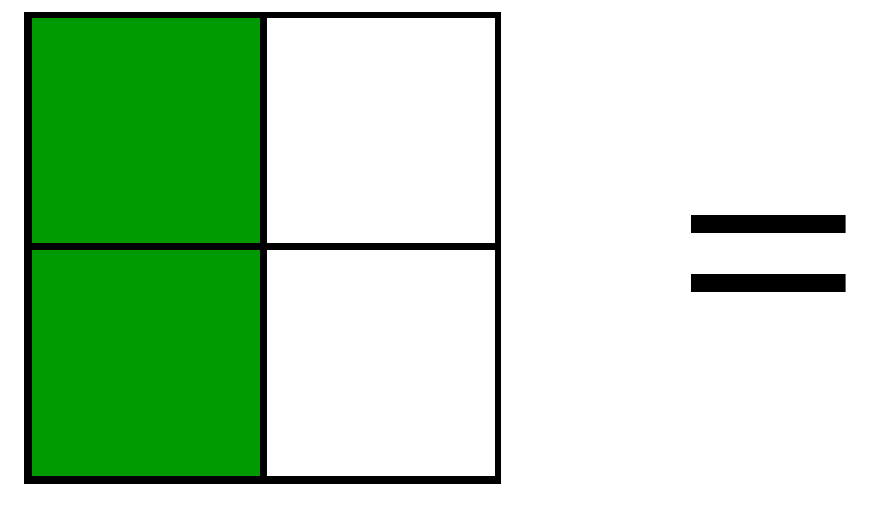
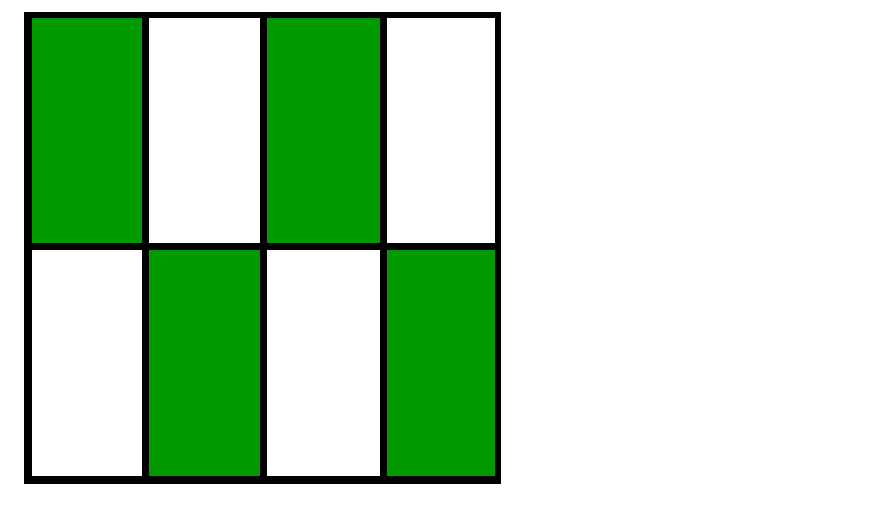
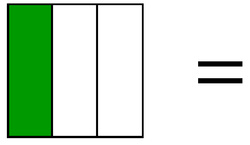
Let's look at how we can divide common shapes to represent different fractions...
It can also be helpful to use a number line to visualize how small or big different fractions are.
|
Many of us have used number lines to solve simple arithmetic puzzles. For example, if someone asked you what 3 + 1 is, you could use a number line to explain to them how if you start with 3 and then add one, you can move down the number line and get to 4. Back in Unit 4 we looked at what was in between the numbers. As we took a closer look we saw numbers that are bigger than 0 but less than 1. These are called decimals. But now, as we investigate further, we can also call label these as fractions! |
|
- Learn About Fractions: Use these interactive lessons to review fraction concepts.
- Pizza Fractions: Use the pizza to review fractions (choose a lower level to start) - Design a Flag: Color your flag using the specified fraction requirements. - Math Magic: Use your mathematical magician skills to help solve these magic tricks! - Fraction Splat: Find the correct fraction and zap it down! - Fraction Match: Match the written fraction to its pictorial model. - Sand Dollar: Help Mr. Crab find the correct fraction for his shells! - Fraction Fling: Find the correct matching faction and use your slingshot to pop the bubble. |
7.2 fractions of Sets
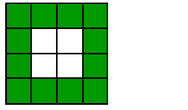
Sometimes the "whole" is not just one shape or one thing. Often we want to look at a group of things as the whole. For example...
Here is a helpful strategy for finding the fraction of a set...
|
|
|
|
- Fraction of a Number: Can you find the fractional part of different wholes?
- Bake a Cake: Help the kids bake a chocolate cake using fractions! - 40 Frogs: How many ways can you show different fractions of a set of 40 frogs? |
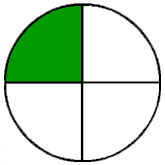
7.3 probabilities when OUTCOMES are equally likely
Probability = how likely it is for an event to happen
Outcomes = the results
Favorable Outcomes = an outcome that satisfies or meets the conditions of the event
Possible Outcomes = the total number of outcomes
Outcomes = the results
Favorable Outcomes = an outcome that satisfies or meets the conditions of the event
Possible Outcomes = the total number of outcomes
To figure out the probability of picking one card at random from the above deck of cards, first we need to know a bit about cards...
- A deck of cards is made up of 52 cards.
- There are 4 suits: clubs, spades, hearts, and diamonds.
- Each suit is made up of 13 cards: 10 number cards, and 3 face cards... a jack, a queen, and a king
- A deck of cards is made up of 52 cards.
- There are 4 suits: clubs, spades, hearts, and diamonds.
- Each suit is made up of 13 cards: 10 number cards, and 3 face cards... a jack, a queen, and a king
What is the probability of picking...
|
a red card?
Out of the 52 total cards, 26 are red.
We would say the likelihood of this event occurring is even or 50:50.
|
a club card?
Out of the 52 total cards, 13 are clubs.
We would say the likelihood of this event occurring is unlikely.
|
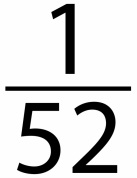
a 5 of ♤?
Out of the 52 cards, only 1 is the 5 of ♤.
We would say the likelihood of this event occurring is very unlikely.
|
|
- Spin It: Use the spinner to see probability in action!
- How Likely: Given different events, can you determine how likely it is they will happen? - Pull From A Bag: Determine the different likelihood of pulling objects from a bag. - Probability Fair: Welcome to the Count Fair! Win some tickets and play the games! |
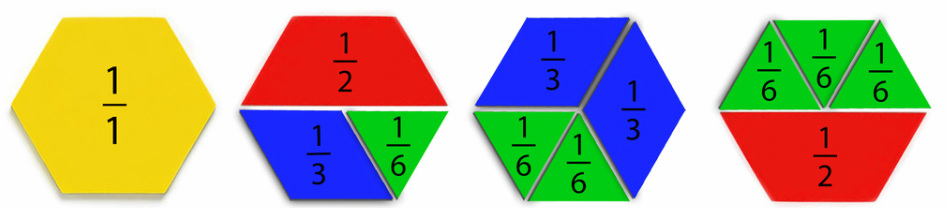
7.4 pattern-block fractions
Pattern blocks are a great way to visualize fractions. Let's start off by looking at different ways to make a whole out of the parts.
1 = 1 1/2 + 1/2 = 1 1/3 + 1/3 + 1/3 = 1 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1
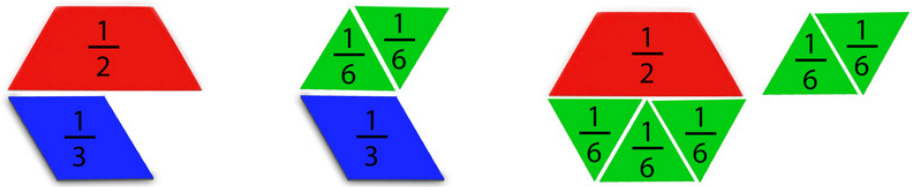
Using the pattern blocks we can also see that it is possible to create a whole by adding different sized parts or fractions together.
1 = 1 1/2 + 1/3 + 1/6 = 1 1/3 + 1/3 + 1/6 + 1/6 = 1 1/6 + 1/6 + 1/6 + 1/2 = 1
|
- Cookie Time: Help frost the geometry shaped cookies!
- Pattern Block Maker #1: Use this shape tool to create any pattern block design you can think of. - Pattern Block Maker #2: Here is another pattern block design program you can use. - Test Time: How well will you score on this fraction test? |
7.5 fraction and mixed-Number addition and subtraction
Adding fractions is an important skill. It can be helpful for many different things: cooking, shopping, baking, building, measuring, etc.
Let's start with adding fractions that have the same denominator...
Let's start with adding fractions that have the same denominator...
Here are a few more examples...
1/6 + 1/6 = 2/6 1/3 + 1/3 = 2/3 1/6 + 1/6 + 1/6 + 1/6 = 4/6
Now let's look at how we can add fractions that have different denominators...
Here are a few more examples...
1/2 + 1/3 = 5/6 1/6 + 1/6 + 1/3 = 2/3 1/2 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 1/3
|
|
|
|
- Fraction Board Game: Roll the dice and travel around the board adding/subtracting fractions!
- MathMan: Navigate your Pacman through the maze and capture the ghosts. - Fruit Shoot: Add the fractions and then shoot the fruit! |
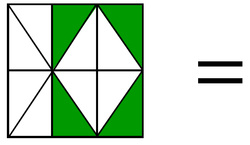
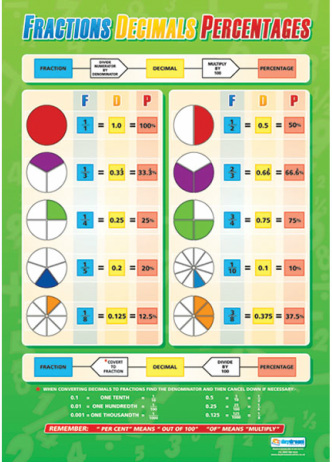
7.6 many names for fractions
Fractions can have many names. For example, look at the different ways that these fractions can be represented visually...
We can also represent these fractions by writing them as equivalent fractions and using different numbers. Take a look...
|
- Soccer Simplification: Simplify the fractions and then try to shoot the ball and make a goal!
- Baseball Simplification: Simply the fractions and then hit a home run! |
7.7 equivalent fractions
|
- Matching Game: Quick... Can you find the equivalent fractions?
- Melvin's Potions: Help Melvin the Wizard find the equal bottles. |
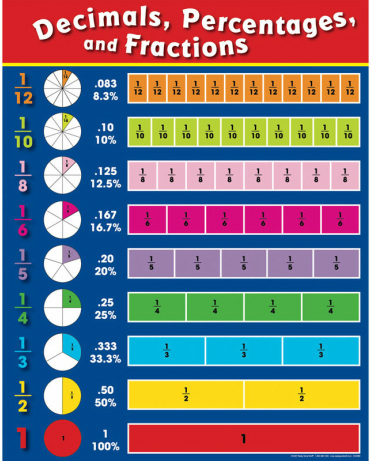
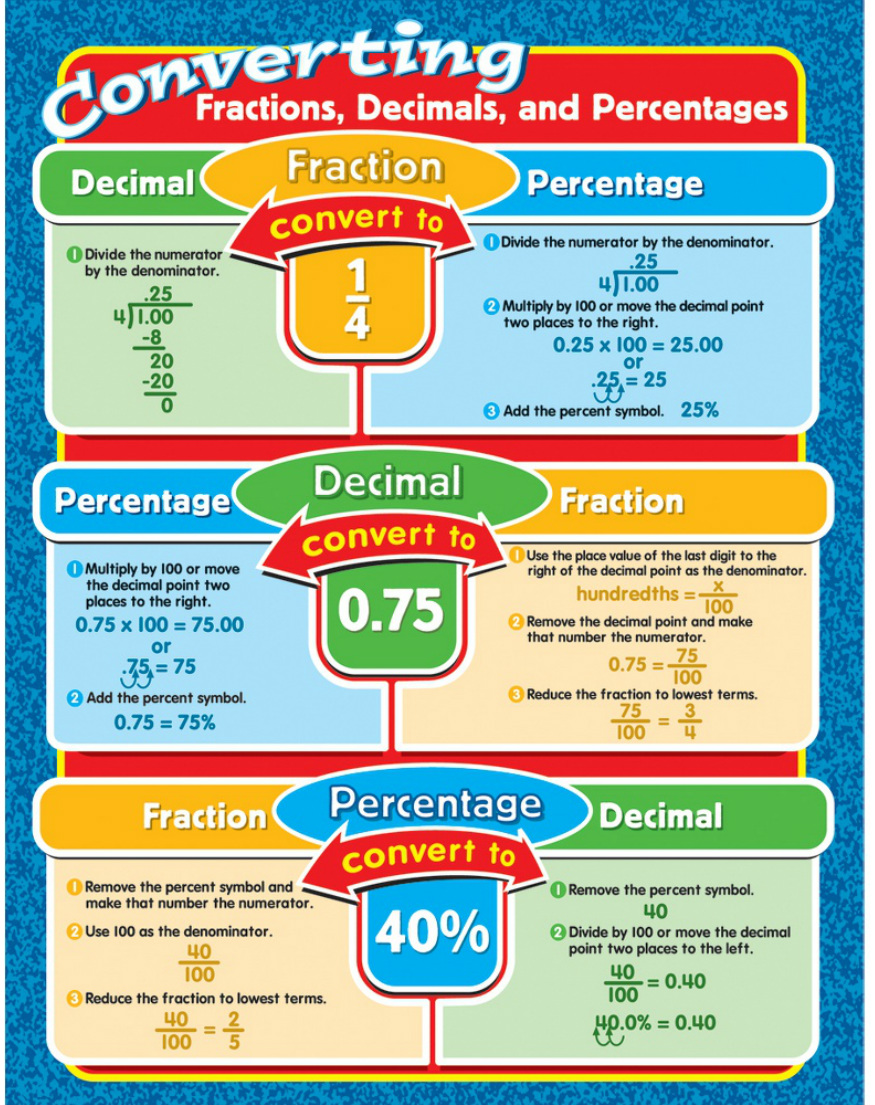
7.8 fractions and decimals
|
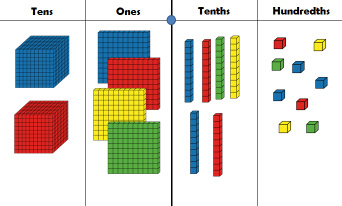
In Everyday Math, you have become very familiar with base-10 blocks.
Let's review how they work... - Ones are represented by cubes - Tens are represented by longs - Hundreds are represented by flats - Thousands are represented by BIG cubes or blocks Now, let's look at the flat as the whole... If we shade in different parts we can represent different fractions... |
|
|
|
|
- Fruit Shoot: Use your knowledge of fractions and decimals to shoot the fruit!
|
7.9 comparing fractions
|
|
|
|
- Dolphin Race: Choose the biggest fraction to win the race!
- Monkeying Around: Hang the monkey fractions in order from lowest to highest. - Hang it Up: Help hang the fraction photos in order these fractions from lowest to highest. |
7.10 the one for fractions
Up to now, we have used the yellow hexagon pattern block as the whole or worth ONE. Now, let's take a look at what happens when we change the ONE. For example, if we say that a yellow hexagon is worth 2/3, then 3 trapezoids would make one whole.
|
- StudyJam: Check out all these resources and games that will help you study fractions.
- Fraction Creator: Use this interactive machine to create your very own fractions. - Quiz Quest: Can you answer all the question correctly? |
7.11 PROBABILITY, fractions, and spinners
|
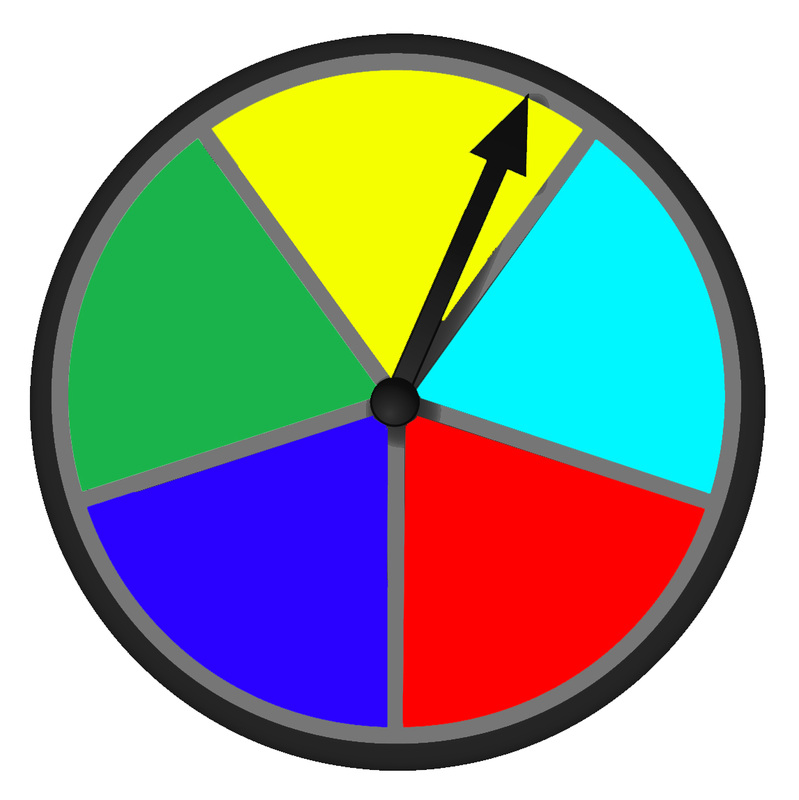
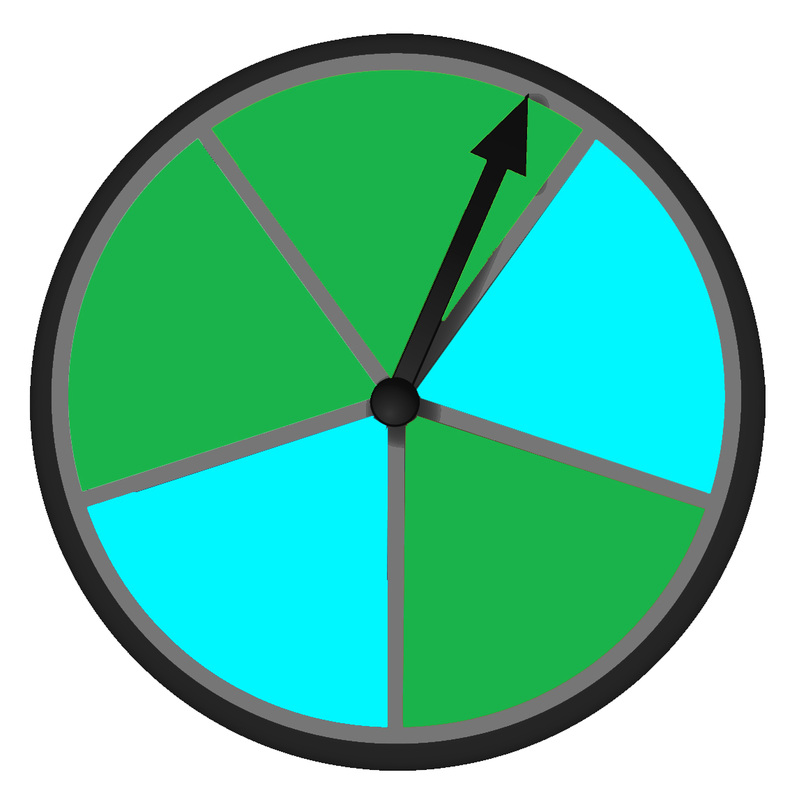
Probability = the likelihood that an event will happen.
Many games use probability to add an element of chance to the game. These devices include dice, coins, and spinners. A fair device means that every outcome is equally likely or has an equal chance of happening. For example, the spinner has a 1/5 chance of landing on any color. In the unfair spinner, the spinner is more likely to land on green than on blue. There is a 3/5 chance of it landing on green and a 2/5 chance of landing on blue. |
Fair Spinner
The spinner has an equal chance of landing on any color in the circle. |
Unfair Spinner
The spinner has an unequal chance of landing on green compared to blue. |
|
|
|
|
- Mission Possible: As a spy, it's your job to save the world using probability!
- Match It: Can you match the probability in fraction form with the correct spinner? - How Likely: Can you determine the probability of each of these different events? - Probability Fair: Welcome to the Count Fair! Win some tickets and play the games! - Probability Pond: Find the probability... before you croak! - Probability Circus: Help the clowns figure out the probability of their colorful spinners! |
7.12 a cube-drop experiment
|
- Jeopardy: Can you name fractions as decimals or percents? Do your best and win some points!
- Alien Antics: On a far away planet, the aliens need your help. |
"Show what you know"
are you ready?
Can YOU write equivalent fractions?
Can YOU write >, <, or = to make each number sentence true?
Can YOU write each set of fractions in order from smallest to largest?
Can YOU use pattern blocks to solve problems?
Can YOU solve fraction problems that involve money?
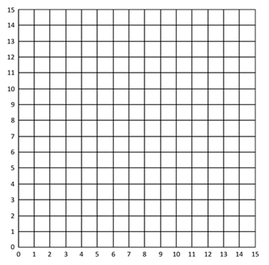
Can YOU plot and label each point on the coordinate grid?
Can YOU write equivalent fractions?
- 1/4 , _________ , __________
- 2/3 , _________ , __________
- 1/7 , _________ , __________
Can YOU write >, <, or = to make each number sentence true?
- 1/8 _________ 1/5
- 2/3 _________ 4/6
- 9/15 _________ 3/6
Can YOU write each set of fractions in order from smallest to largest?
- 1/8 , 4/8 , 2/8 , 7/8 , 5/8 smallest ________ , ________ , ________ , ________ , ________ largest
- 2/7 , 2/5 , 2/9 , 2/6 , 2/4 smallest ________ , ________ , ________ , ________ , ________ largest
Can YOU use pattern blocks to solve problems?
- If the blue rhombus is the whole, what fraction is one green triangle? _________
- Suppose the green triangle is 1/2 of the whole. Which pattern block is 1 whole? _________________________
Can YOU solve fraction problems that involve money?
- Jake had 12 quarters He spend 1/4 of them on a pack of gum.
- How many quarters did he spend? __________
- How many quarters does he have left? _________
- How much money does he have left? __________
- A bag contains 2 blue marbles, 3 orange marbles, 3 red marbles, and 3 yellow marbles. You put the marbles in a bag and mix them up. About what fraction of the time would you expect to pull out a red marble? ___________
Can YOU plot and label each point on the coordinate grid?
Can YOU multiply and divide using any algorithm of your choice?
- 39 x 37 Answer: _______________
- 43 x 31 Answer: _______________
- 87 ÷ 6 Answer: _______________
- 576 ÷ 43 Answer: _______________
Can YOU explain a strategy to compare fractions?
- Which fraction is larger? 3/4 or 9/10 Explain.
|
Can YOU create a spinner and predict the probability of an event?
|
Can YOU add or subtract fractions and mixed numbers?
Can YOU solve a fraction number story?
- 1/6 + 1/12 Answer: _______________
- 2 1/5 + 1 1/3 Answer: _______________
- 2 2/3 - 1 2/6 Answer: _______________
- 1/2 - 1/8 Answer: _______________
Can YOU solve a fraction number story?
- It took Matt 4/6 of an hour to drive from Okemos to Lansing and 1/2 hour to drive from Lansing to Grand Ledge. To figure out his total driving time, Matt wrote the following number model: 4/6 + 1/2 = 5/8
Do you agree that his trip took him about 5/8 of an hour? Explain.