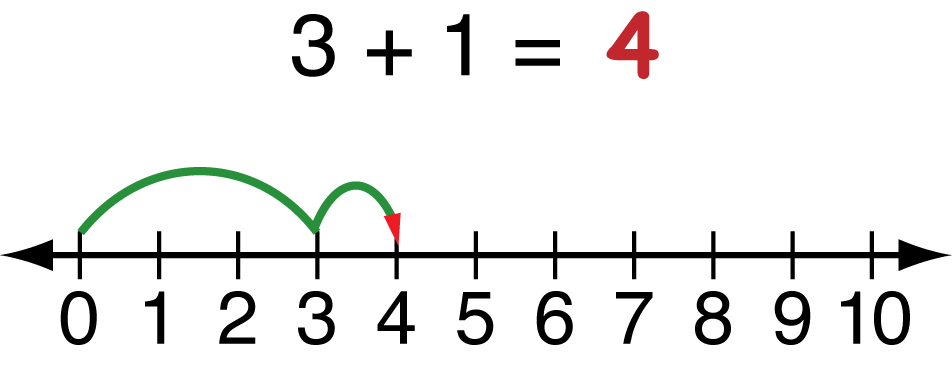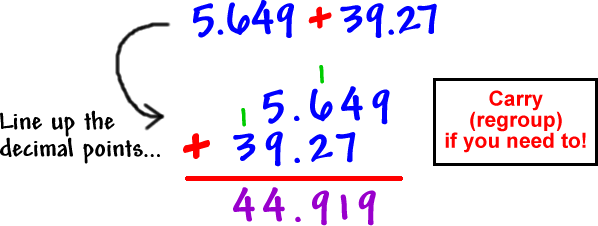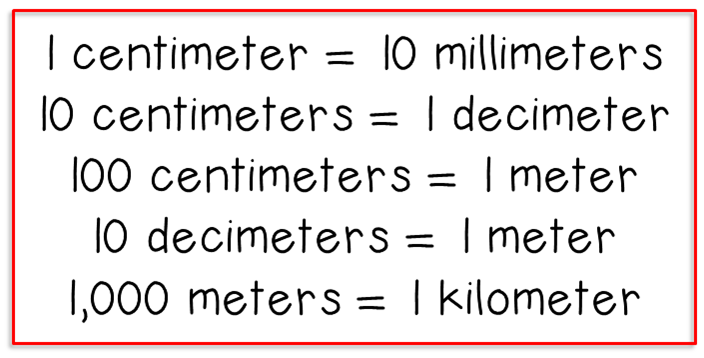decimals and their uses
4.1 Decimal place value
Number Line: A line on which numbers are marked at intervals.
|
Many of us have used number lines to solve simple arithmetic puzzles. For example, if someone asked you what 3 + 1 is, you could use a number line to explain to them how if you start with 3 and then add one, you can move down the number line and get to 4.
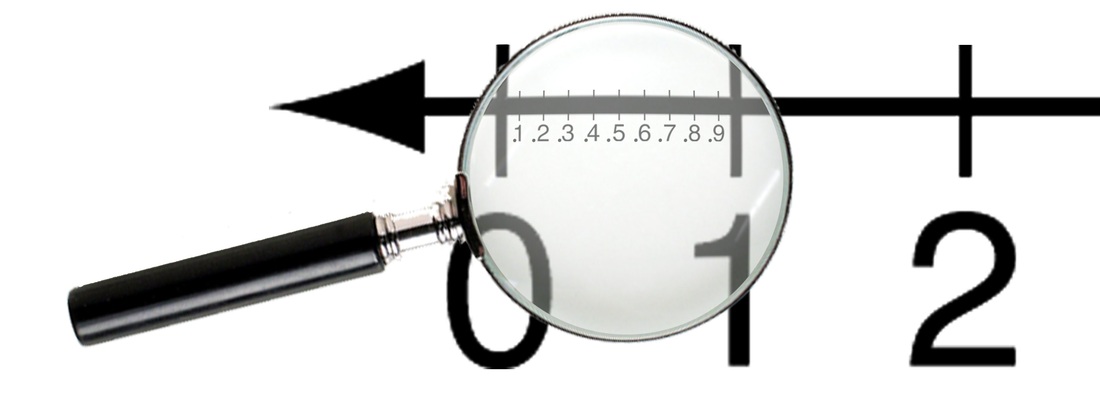
But have you ever thought about what was in between the numbers? What would we see if we took a magnifying glass to get a closer look? We can see that when we look at our number line in more detail we can see numbers that are bigger than 0 but less than 1. These are called decimals. Looking at this we can tell that 10 is ten times as much as 1, and that 1 is ten times as much as 0.1 and so on. What would we see if we got out another magnifying glass and zoomed in to see what is between 0 and 0.1? |
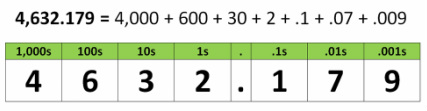
In order to understand place value of decimals, let's go back and remember place-value of whole numbers. For example, in the number 1,234 the digit 1 is in the thousands place - its value is 1 thousands or 1,000. The digit 3 is in the tens place - its value is 3 tens, or 30.
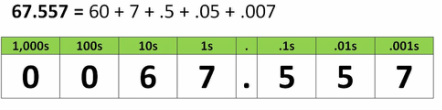
In whole numbers, each digit represents a specific amount depending on which place it is in. The same is true for decimals!
In whole numbers, each digit represents a specific amount depending on which place it is in. The same is true for decimals!
|
- Scooter Quest: Help Jimmy earn money to buy a new scooter by choosing the right decimal garage.
- Football Pass: Pass the ball and answer the decimal question to score a touch down! - Pirate Place Value: Arrrg! Ye ready to fight them pirates and find the buried treasure? |
4.2 Review of basic decimal concepts
|
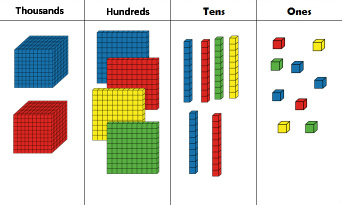
In Everyday Math, you have become very familiar with base-10 blocks.
Let's review how they work... - Ones are represented by cubes - Tens are represented by longs - Hundreds are represented by flats - Thousands are represented by BIG cubes or blocks Using that information we can say that... 1 flat = 10 longs (because 100 = 10 x 10) 1 long = 10 cubes (because 10 = 1 x 10) 1 flat = 100 cubes (because 100 = 1 x 10 x 10) |
|
You may also have become familiar with fractions. Let's review how they work... A fractions is always a fraction of "something." In these examples we refer to this "something" as the ONE, or the WHOLE. |
James ate 1/2 a pizza.
The pizza is the ONE. |
Michelle used 2/3 cup of pineapple in her recipe.
The cup is the ONE. |
Eric used 1/4 of the crayons in his box.
The box of crayons is the ONE. |
|
What if we change the way we think about base 10 blocks?
If we think of a flat as the ONE... then what fraction of a flat is a long? - 1/10 because 10 longs = 1 flat. [This can also be written as 0.1] If we think of a flat as the ONE... then what fraction of a flat is a cube? - 1/100 because 100 cubes = 1 flat. [This can also be written as 0.01] If we think of a flat as the ONE... then what fraction of a flat is 3 longs? - 3/10 because 10 longs = 1 flat. [This can also be written as 0.3] |
|
- Fraction Shooter: Blast the fractions right out of the sky.
- Decimals of the Caribbean: Sink those decimal ships! |
4.3 comparing and ordering decimals
|
If we are looking at two decimal numbers we might want to compare them. We can do this by figuring out if the number is either greater than, less than or equal to the other number.
A decimal number is just a fractional number. Comparing 0.7 and 0.07 is clearer if we compared 7/10 to 7/100. The fraction 7/10 is equivalent to 70/100 which is clearly larger than 7/100. Therefore, when decimals are compared start with the tenths place and then hundredths place, etc. If one decimal has a higher number in the tenths place then it is larger than a decimal with fewer tenths. If the tenths are equal compare the hundredths, then the thousandths etc. until one decimal is larger or there are no more places to compare. If each decimal place value is the same then the decimals are equal. |
|
Use the number line below to try and figure out which decimal goes where.
|
Let's try and figure out what number letter b represents.
We can see that it is between 0 and 1, so we know it is going to be less than 1 but bigger than 0. We can also see the number line is broken up into tenths and b falls between 0.2 and 0.3 so we need to find a number that is between. 0.25 is between so b = 0.25 |
|
- Fruit Shoot: Compare the decimals and then blast the fruit with the correct relation symbol.
- Compare The Decimals: Greater Than, Less Than, or Equal To... YOU decide! - Decimal Jeopardy: "I'll take decimals for 300 please!" How many points can you rack up? - Decimal Balloon Pop: Pop the balloons in order from least to greatest. - Order the Decimals: Put the decimals in order. - Beat the Timer: Order the decimals before time runs out. |
4.4 estimating with deciamls
|
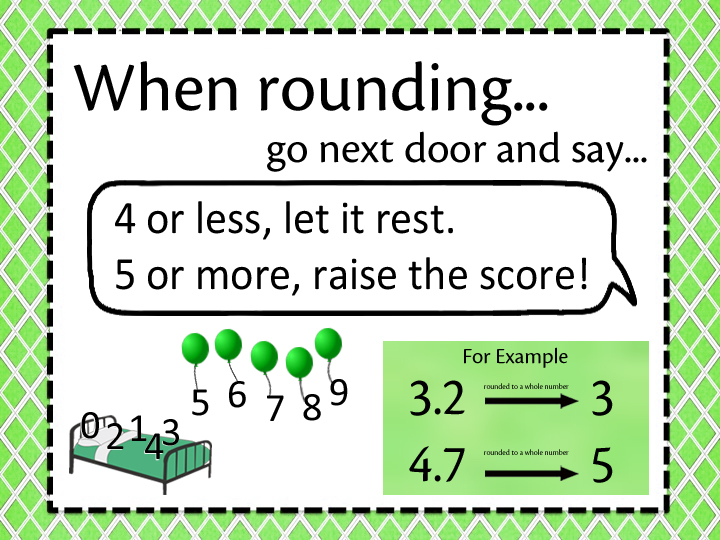
Estimating can be a very useful tool for solving number puzzles. Just like when we estimate whole numbers, we want to choose "close-but-easier" numbers that we can add in our heads easily. For example, if I wanted to add 1,890 + 2,102 I would want to use estimation to may check my answer or get a ball park idea of the answer. I would round 1,890 to 2,000 and 2,102 to 2,000. Now it is much easier to add 2,000 + 2,000 = 4,000 The same can work for decimals... If I needed to add 3.56 + 2.7 and 8.4 I could use estimation to a quick ballpark idea of an answer. I would round 3.56 to 4, 2.7 to 3, and 8.4 to 8. Now it is much easier to add 4 + 3 + 8 = 15 |
|
|
|
|
- Baseball Home Runs: Round the decimals to hit a home run!
- Half Court Rounding: Round the decimals and make a 3-point swish! |
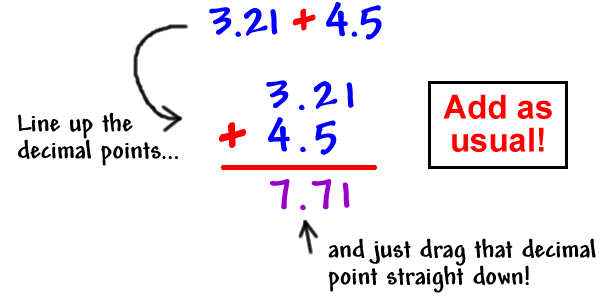
4.5 decimal addition and Subtraction
|
When you add or subtract decimals... - First... line up the decimals! - Then... bring down the decimal point. - Next... put zeros in and fill the gaps (only if necessary). - After... start adding and subtracting! - Lastly... check your answer. |
|
how to add decimals |
how to subtract decimals |
|
- Basketball Slam Dunk (Addition): Add the decimals and then shoot the ball.
- Baseball Home Run (Addition): Add the decimals to hit a home-run. - Basketball Slam Dunk (Subtraction): Subtract the decimals and then shoot the ball. - Baseball Home Run (Subtraction): Subtract the decimals and then hit a home-run. - Railroad Repair: Can you help the Cyberchase gang fix the railroads. |
4.6 decimals in Money
Introducing Bank Accounts
- Deposit = when money is put into an account.
- Withdrawal = When money is taken out of an account.
- Balance = The amount of money in an account.
- Interest = The amount of money a bank adds to an account for letting them use the money.
|
- Money Math: Use the cash register to figure out the change!
- ATM Adventure: What is it like to use an ATM? Practice using this real life simulation. - Balance the Checkbook: Can you solve this money madness? Hurry and balance the account! - The Lunch Lady: You will have to be quick to add up the cost of these hungry kids' lunches! - Making Change: Your customers are in a hurry. Give them the right amount of change and quick! |
4.7 thousandths
|
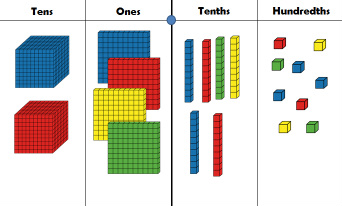
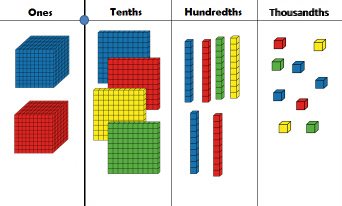
The last time we looked at base 10 blocks, we thought of a flat as the ONE.
What if we change the way we think about base 10 blocks again? If we think of a block as the ONE... then what fraction of a block is a flat? - 1/10 because 10 flats = 1 block. [This can also be written as 0.1] If we think of a block as the ONE... then what fraction of a block is a long? - 1/100 because 100 cubes = 1 block. [This can also be written as 0.01] If we think of a block as the ONE... then what fraction of a block is a cube? - 1/1000 because 1,000 cubes = 1 block. [This can also be written as 0.001] |
4.8 metric units of length
|
- The numbers stand for centimeters.
- The smallest marks stand for millimeters. - There are 10 millimeters in 1 centimeter. - There are 10 centimeters in 1 decimeter. - There are 100 millimeters in 1 decimeter. - There are 10 decimeters in 1 meter. - There are 100 centimeters in 1 meter. - There are 1,000 millimeters in 1 meter. |
Symbols for Metric Units
mm = millimeter(s) cm = centimeter(s) dm = decimeter(s) m = meter(s) |
|
|
|
|
- Metric Mash-Up: Match up the metric measurements and level up!
|
4.9 personal references for metric length
It is hard to remember how long a centimeter or a foot is, how much area a square yard takes up, or how heavy a pound feels. Relating measures to common objects makes it easier to remember their relative sizes. Sometimes we need to measure something but don't have a tool. Personal measurement references can be used to estimate the unknown measurement.
|
- Measurement Unit Quiz: How well do you know your units of measurement?
|
4.10 measuring in Milimeters
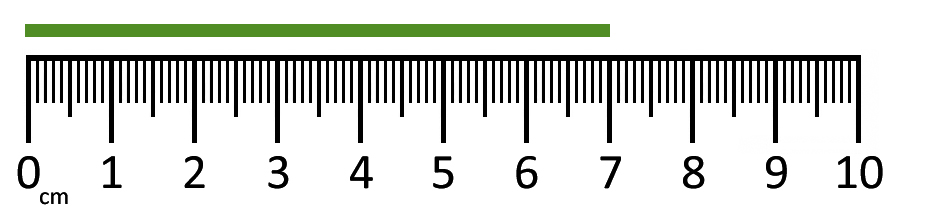
The line segment below measures 7 cm.
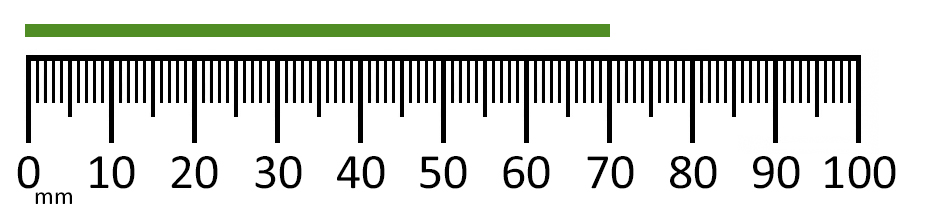
The line segment below measures 70 mm.
The two lines above are exactly the same size. This helps us to see that for every 1 cm there are 10 mm.
So... this line measures 70 mm or 7 cm
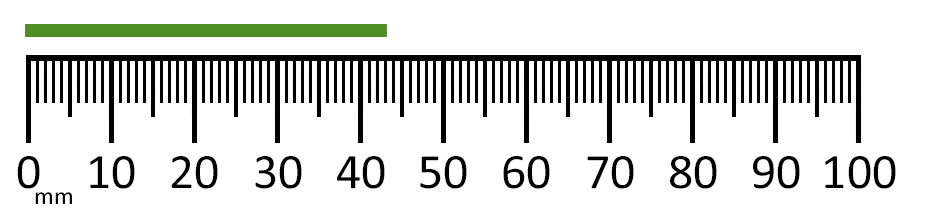
Can you measure this line segment to the nearest mm?
This line measures 43 mm or 4.3 cm
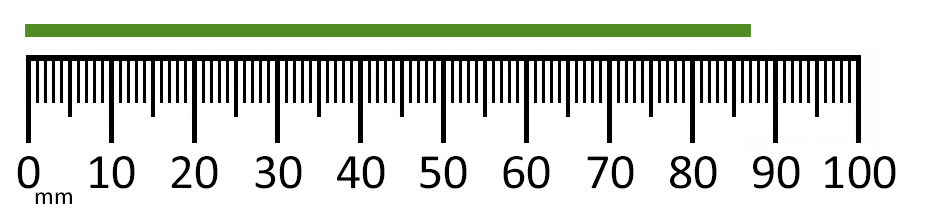
Can you measure this line segment to the nearest mm?
This line measures 87 mm or 8.7 cm
What about this line segment? Even though the ruler is marked in cm, you can still measure it in mm!
Remember, 1 cm = 10 mm
So... this line measures 35 mm or 3.5 cm
So... this line measures 35 mm or 3.5 cm
|
- Measure Mayhem: Choose the right measurement.
- Build a Shed: Figure out the correct measurements needed to build your shed. - The Ruler Game: How fast can you read the ruler? |
"Show what you know"
are you ready?
Can YOU use a relation symbol (<, >, =) to make the number sentence true?
- 2.50 ______ 2.05
- 7.980 ______ 6.29
- 4.5 ______ 5.4
- 4.900 ______ 4.9
Can YOU write the following numbers in order from largest to smallest?
- [ 3.2, 8.0, 5.54, 0.04, 0.4, 1.02 ]
- ______ ______ ______ ______ ______ ______
- ______ ______
- ______ ______
Can YOU measure a line segment to the nearest centimeter?
- _________________________________________________________ = about ______ cm
- ___________________________________________________________________________________ = about ______ cm
Can YOU measure a line segment to the nearest 1/2 centimeter?
- ___________________________________________________________________________________________________________ = about ______ cm
- _______________________________________ = about ______ cm
Can YOU list the first 10 multiples of the number 6?
- ______ ______ ______ ______ ______ ______ ______ ______ ______ ______
- __________________________
- ______ and ______ ______ and ______ ______ and ______ ______ and ______
Can YOU tell if 16 is a prime number or a composite number?
- ________________________
Can YOU add or subtract these decimals mentally or with a paper-and-pencil algorithm?
- $2.39 + $3.83
- 2.98 + 39.2
- 311.923 + 8.230
- 2.3 - 2.300
- 1.892 - 0.983
- $4.54 - $3.53
- f + 54 = 137 f = _______
- 2 * d = 62 d = _______
- 100 / j = 25 j = _______
- 138 - g = 58 g = _______
Can YOU write each decimal as a fraction?
- 0.63 = ________
- 0.8 = ________
- 0.654 = ________
- 0.800 = ________
- 0.1 = ________
- _________________________________________ = ______ mm or ______ cm
- ______________________________________________________________________ = ______ mm or ______ cm
Can YOU solve this number story?
- James went to the bank and deposited $89.00 dollars into his account on Monday. Then on Wednesday he withdrew $33.45 and then on Thursday he deposited $19.28. If his balance at the end of the week is $340.84, what was his balance at the start of the week? Explain.
Can YOU solve this number story?
- Amy was working with base-10 blocks. She was using the flats as the ONE. The longs were tenths and the cubes were hundredths. She counted 14 cubes - "one-hundredth, two-hundredths, three-hundredths, four-hundredths, five-hundredths, six-hundredths, seven-hundredths, eight-hundredths, nine-hundredths, ten-hundredths, eleven-hundredths, twelve-hundredths, thirteen-hundredths, fourteen-hundredths." She wrote down 0.014 to show what the blocks were worth. Is Amy right? Explain.