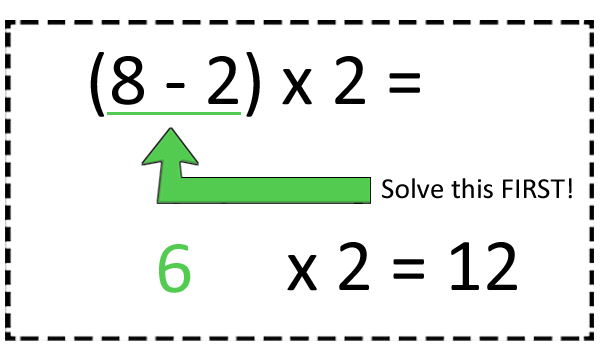Multiplication and Division, Number Sentences and Algebra
3.1 "What's My Rule"
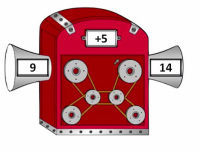
Mr. C was working late in his classroom one night, when he discovered a mysterious machine hiding in the back of his closet. He got it out and set it on his half doughnut table. It clearly hadn't been used in a long time because it was really dusty. As he brushed it off he noticed a label on the top that said "Function Machine: Put in a number and get a NEW number out." Curious, Mr. C decided to put in the number 3. The machine instantly came to life - gears spun - lights flashed - and the machine made strange "beep - boop - beep" noises. Before Mr. C could even react, the machine spit out the number 8 on the other side. Intrigued by the machine, Mr. C decided to try it again. This time he put in the number 9. Again the machine whistled, flashed, and beeped until it spit out the number 14. "Interesting!" Mr. C exclaimed. "I think I see what this machine does. If I put in a number, it adds more to give me a bigger number. But what does it add? Hmmm... this is still unknown. Well, 8 is 5 more than 3, and 14 is 5 more than 9. So, the machine must add 5 to the first number and then gives me the new number. If I am right, I can put in the number 15 and I should get 20 out!" Mr. C put a 15 into the machine. The machine went whiz, whirl, beep, boop, beep and to his delight, a 20 spit out!
|
How a Function Machine works...
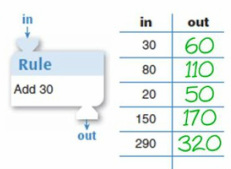
- A number (the input) is dropped into the machine. - The machine changes the number according to a rule. - The new number (the output) comes out at the other end. In this example, the Function Machine's rule is +5 which means that when any number is dropped into the machine, the machine will add 5 to it and give a new number out that is 5 more than the original input. 12 + 5 = 17 |
|
|
|
|
- The Function Machine: Can you figure out the rules for these function machines?
- Stop the Creatures: Help the Cyberchase gang stop Hacker's clones by cracking his machine's code. |
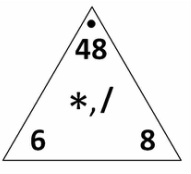
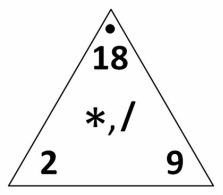
3.2 Multiplication facts
|
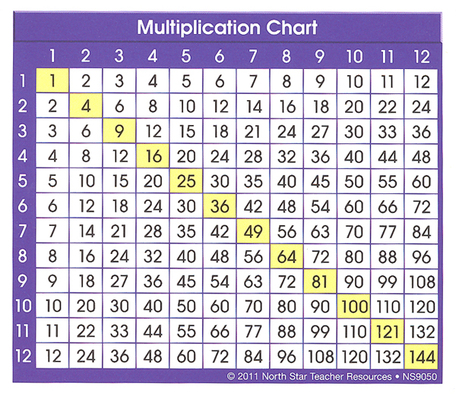
Factors = The numbers in the shaded purple row and column. These numbers when multiplied together equal a product.
Example: 2 x 7 = 35 Products = The rest of the numbers. The result of multiplying two factors together. Example: 6 x 7 = 35 Factor Pairs = A specific pair of numbers that when multiplied together equal a specific product. Example: 6 and 7 are factor pairs of 35. Multiples = The numbers across a row or down a column. Example: the multiples of 6 are 6, 12, 18, 24... Square Numbers = The numbers highlighted in yellow. The product of multiplying a factor by itself. Example: 36 = 6 x 6 , 81 = 9 x 9 , 16 = 4 x 4 |
factors |
multiples |
Prime Numbers = Numbers with only one factor pair. (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71...)
Composite Numbers = Numbers that are not prime.
|
- Pumpkin Multiples: Can you catch all the pumpkins that are multiples of your number?
- Multiple Venn-Diagram: Sort the multiples of two numbers into a Venn-Diagram. - Shooting Factors: Shoot the marble at its factor pair before time runs out. - Using a Multiplication Table: Use this interactive multiplication table to practice your math facts. - Who Wants to be a Millionaire (Factor Edition): If you know factors, you might just earn $1,000,000! - Broken Calculator: Eric has smashed his calculator, but some of it still works. Can you help him? - Is It Prime? - Enter any number you can think of and see if it is prime! - Multiple Ninja: Slice the multiples and save the day! - Meteor Madness: Shoot the meteors before they destroy your ship! |
3.3 Multiplication fact Practice / 3.4 MORE multiplication practice
Memorizing multiplication facts allows you to solve problems you encounter in every day life. For example, to determine how many cupcakes are in 6 package with 6 cupcakes per package, you use multiplication to solve the problem. Also, it makes doing math much easier. If you have to stop and think what 7 x 8 is when you are solving a problem, it slows you down. You are more likely to make a mistake or lose track of what you are doing. Being able to quickly know your basic multiplication facts is a skill that will last a lifetime!
|
Mystery Numbers
A Mystery Number is a number that can be found out using clues. Often they are written as word problems, but they can also be number sentences as well. |
I am thinking of a mystery number. If I multiply it by 5, the answer is 30. What is the number? [ 6 ]
I am thinking of a mystery number. If I multiply it by 8, the answer is 56. What is the number? [ 7 ] I am thinking of a mystery number. This number is 4 times as many as 9. What is the number? [ 36 ] I am thinking of a mystery number. This number is 2 times as many as 4. What is the number? [ 8 ] |
PRIME / COMPOSITE REVIEW:
Prime Numbers = Numbers with only one factor pair. (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71...)
Composite Numbers = Numbers that are not prime.
Prime Numbers = Numbers with only one factor pair. (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71...)
Composite Numbers = Numbers that are not prime.
|
- Math Magic: Are you a Multiplication Math Magician?
- Math Match: Can you match the factors to their product? - Multiplication Mash-Up: A website with A LOT of fun multiplication games! - Flash Card Practice: Use these flashcards to practice your multiplication facts. - Study Smart: A great resource for printable flashcards, quizzes, and links to math fact apps. - Math Mayhem: Try to beat other players by knowing your math facts faster! - Flappy Bird: Help Flappy Bird fly through the tubes by choosing the right gap. Be warned. It's hard! - Tony's Tires: Use your knowledge of fast facts to win the race! |
3.5 Multiplication and Division
|
- Division Games: There are A TON of division games here to practice your division and fact families.
- Fruit Splat - Division: Shoot the right fruit to score the points! Can you get the high score? - Broken Calculator: Can you help Eric fix his broken calculator? |
3.7 Finding Air Distances
|
|
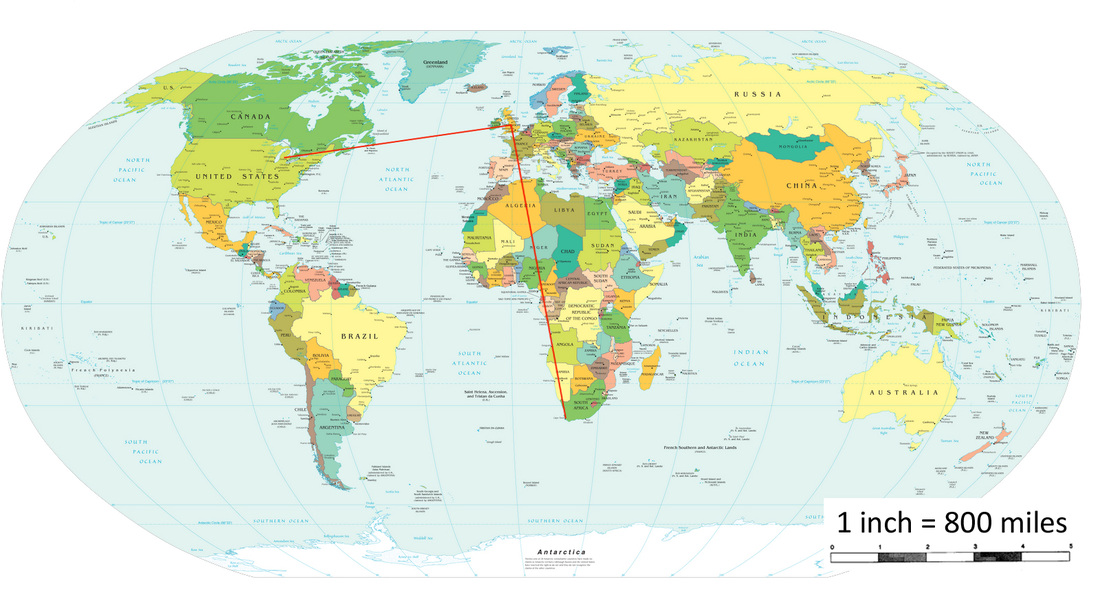
This weekend, Mr. C. decides he wants to take a quick trip to South Africa and see the giraffes! South Africa is a very far away, so he decides that he is going to fly. But before he can go, he must figure out how many miles it will take to get there. Good thing he knows how to calculate air distance.
Mr. C. gets out his world map and finds Lansing, Michigan and Cape Town, South Africa. He knows that the shortest distances between these two points is a straight line, but he also realizes that there aren't any flights that will take him straight from Lansing to Cape Town. So, he decides that he will have to make a pit stop in London, England. Using the map key, Mr. C. notices that 1 inch = 800 miles. He knows that this means that for every inch represented on the map, it is actually 800 miles in real life. Mr. C starts by measuring the distance from Lansing to London with his ruler and he gets 4.75 inches. To figure out how many miles that is, Mr. C knows he needs to multiply that by 800 miles. 4.75 x 800 = 3,800 miles from Lansing to London. Mr. C then measures the distance from London to Cape Town with his ruler and he gets 6.5 inches. Again, he knows he must multiply this by 800 to get the total actual miles. 6.5 x 800 = 5,200 miles from London to Cape Town. When he adds it all up, his total round trip from Lansing to Cape Town and back will be about 18,000 miles! (3,800 + 5,200 + 5,200 + 3,800 = 18,000) |
3.8 A Guide for Solving Number Stories
Number Story: A story with a problem that can be solved with arithmetic.
number problem guideNumber problems can often be very challenging. It is best to have a strategic plan of attack when trying to figure out these kinds of puzzles. Following these steps may be very useful.
1. UNDERSTAND THE PROBLEM - Read the problem. Can you retell it in your own words? - What do you want to find out? - What do you know? - Do you have all the information needed to solve the problem? 2. PLAN WHAT TO DO - Is the problem like one that you solved before? - Is there a pattern you can use? - Can you draw a picture or a diagram? - Can you write a number model or make a table? - Can you use counters, base-10 blocks, or some other tool? - Can you estimate the answer and check if you are right? 3. CARRY OUT THE PLAN - After you decided what to do, do it. - Be careful and don't rush. Take your time solving it. - Make a written record of what you do. - Answer the question. 4. LOOK BACK - Does your answer make sense? - Does you answer agree with your estimate? - Can you write a number model for the problem? - Can you solve the problem in another way? |
for example . . ."Mr. C. traveled from Colorado to Maine. He traveled 586 miles on Monday, 487 miles on Tuesday, 630 miles on Wednesday, and 373 miles on Thursday. How many total miles did he travel?"
1. UNDERSTAND THE PROBLEM - What is Mr. C. doing? - He is taking a trip." - What is the question in the problem? - "How far did he travel?" - What details are given about Mr. C.'s Trip? - "The amount of miles he traveled each day: 586, 487, 630, 373." 2. PLAN WHAT TO DO - How could I solve this problem? - "Make a table, draw a picture, make a list, or make a diagram." - Which method will I choose? - "I will make a table and then add up the miles for each day." 3. CARRY OUT THE PLAN - Monday: 586 - Tuesday: 487 - Wednesday: 630 - Thursday: 373 - 586 + 487 + 630 +373 = 2,076 miles. 4. LOOK BACK - Does the answer make sense? - "Yes. The total number of miles is more than any one day." - Number model: 586 + 487 + 630 +373 = m |
|
- Grand Slam Math (Addition / Subtraction): Can you hit a home run with these word puzzles?
- Grand Slam Math (Multiplication / Division): Can you hit a home run with these word puzzles? |
3.9 true or false number sentences
Number Sentences = Two expressions with a relation symbol ( <, >, =).
|
18 > 5 "Eighteen is greater than five." 20 < 53 "Twenty is less than fifty-three." 8 = 8 "Eight equals eight." |
|
Number sentences can also be identified as TRUE and FALSE. For example, 4 x 5 = 20 is a TRUE number sentences because we know that 4 x 5 is 20 and 20 = 20. However, a number sentence like 12 / 4 = 4 is FALSE because we know that 12 / 4 = 3 and 3 is not equal to 4.
|
15 + 13 = 28
This is a TRUE number sentence because 15 + 13 equals 28. |
8 = 5 x 3
This is a FALSE number sentence because 15 x 3 equals 15 not 8. |
25 - ? = 15
You can't tell if this number sentence is TRUE or FALSE because it is missing information. |
8 x 6
This is NOT a number sentence because there is not a sign of equality (<, >, =). |
|
- Raceway: Compare numbers and then drive through busy traffic collecting coins.
|
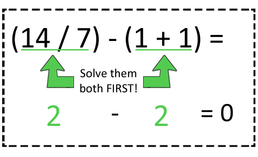
3.10 Parentheses in number sentneces
Parentheses: A mathematical symbol with tell you which part of the problem to do first. When solving a problem, you must always do what is inside the parentheses first in order to solve the puzzle correctly.
|
28 - 6 + 9 = 31
28 - (6 + 9) = 13 |
In this example, this puzzle looks like those that we have typically solved in the past. We simply start on the left and work our way over to the right. So, 28 - 6 is 22 and 22 + 9 gives us 31.
However, when we add parentheses around the 6 + 9 this changes things. We must now do this part first. So (6 + 9) is 15 and now we can do 28 - 15 and it gives us 13. |
|
- Printable Practice: A printable parentheses worksheet. Use the answer key to check your work.
- Make 24: Use parentheses along with the help of +, -, x, and ÷ to make the number 24! - Bracket Basics: Can you figure out what numbers go in the boxes? - High Stakes Heist: Can you use order of operations to crack the safe and grab the money? - Royal Rescue: Will you be the hero of the kingdome? |
3.11 open number sentneces
|
Variables = A letter or symbol that stands for a missing number.
Open Sentence = A sentence that has a variable in it. Solution = The number that makes the number sentence TRUE! For example... 3 + y = 13 The number that would make this number sentences true is 10. So, y = 10 and 3 + 10 = 13 For example... k * 8 = 24 The number that would make this number sentences true is 3. So, k = 3 and 3 * 8 = 24 |
|
|
- Open Sentence Practice: How many open sentences can you solve?
|