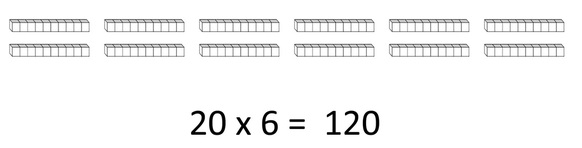Big numbers, Estimation, and COMPUTATION
5.1 Extended Multiplication Facts
|
Mr. C loves chocolate chip cookies. He was walking through the store one day and noticed that they had chocolate chip cookies on sale! His stomach grumbled with hunger when he saw the large chocolaty chunks sticking out of the cookie. He looked at the sign and saw that they were on sale for 20¢. What a bargain he thought to himself. They looked so delicious that he decided to buy 6 cookies! If the cookies were on sale for 20¢ each, what was the total cost that Mr. C would have had to pay for his cookies?
|
There are a lot of different ways we could try to solve this puzzle...
|
Repeated Addition
20¢ + 20¢ + 20¢ + 20¢ + 20¢ + 20¢ = 120¢ or $1.20 Array Pictures Using base-10 blocks, show 6 columns of 2 longs (tens) in each column. 
10 Times-As-Many
If each cookie cost only 2¢ each, then 6 cookies would be 6 x 2¢, or 12¢. Because the cookies cost 20¢ each, 6 cookies must cost 10 times as much; that is 10 x 12¢ = 120¢, or $1.20. Multiplication Comparison What amount is 6 times as much as 20¢? 120¢ or $1.20. |
Many times when we are trying to solve a puzzle, we are challenged with having to complete a task that, at first, can seem hard. Multiplying by larger numbers for example can introduce added challenges. But, the great thing about solving these kinds of puzzles is that there are always easier ways of solving them if we think about them in new or different ways.
For example, we all know that 2 x 3 = 6. This is a basic arithmetic fact that we all understand very well in 4th grade. However, when we start to try to solve puzzles like 2 x 30 this can be a bit more challenging because the numbers are bigger and harder to visualize or count on our fingers. BUT, if we know the shortcuts, this puzzle can be a piece of cake to solve.
|
2 x 30 = ? |
|
Think Money
30¢ = 3 dimes and 2 x 3 dimes is 6 dimes, or 60¢ Multiples of 10 = "tens" 2 x 30 = 2 x 3 tens, which equals 6 tens, or 60 |
|
30 x 50 = ? |
|
Think Money
50¢ = 5 dimes and 30 x 5 dimes is 150 dimes' 150 dimes equals 1,500 cents, so 30 x 50 = 1,500 Multiples of 10 = "tens" Three 5s equal 15, so three 50s is 10 times as much, or 150. Thirty 50s is 10 times as much as 150, or 1,500. |
|
|
Original Fact: The basic arithmetic fact that we begin with.
Extended Fact: Variations of basic arithmetic facts involving multiples of 10,100 and so on. For Example: Original Fact: 4 x 6 = 24 Extended Fact: 40 x 6 = 240 Original Fact: 7 x 9 = 63 Extended Fact: 70 x 90 = 6,300 Original Fact: 2 x 7= 14 Extended Fact: 2 x 700 = 1,400 |
|
- Make Your Own Worksheet: Build your own practice worksheet. Answer key included!
- Splash Time: Use your multiplication knowledge to sail across the splashing sea. - Who Wants To Be A Millionaire: Can you get to the million dollar question? |
5.2 Multiplication Wrestling
DIRECTIONS:
- Grab any deck of regular playing cards. Remove all Kings, Queens, Jacks, Tens, and Jokers so that you are only left with 1-9 cards. (Aces = 1)
- Shuffle the deck of cards and place the deck number-side down on the table.
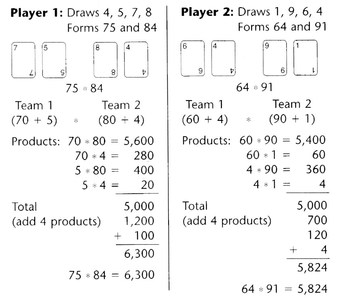
- Each player draws 4 cards and forms two 2-digit numbers. Players should form their 2 numbers so that their product is as large as possible.
- Players create 2 "wrestling teams" by writing each of their numbers as a sum of 10s and 1s.
- Each player's 2 teams wrestle! Each member of the first team is multiplied by each member of the second team. Then the 4 products are added.
- The player with the larger product wins the round and receives 1 point.
- To begin a new round, each player draws 4 new cards to form 2 new numbers. A game consists of 3 rounds.
|
|
EXAMPLE:
|
|
- Multiplication Wrestling: Instructions and a printable game board.
|
5.3 Estimating Sums
|
Mr. C loves the state of Michigan and decided it would be fun to take a week long trip across Michigan! He would visit his family in Midland, see the giraffes at Binder Park Zoo in Battle Creek, and go to a Tiger's Game in Detroit. Mr. C decided that if he was going to drive all over Michigan, he wanted to do it in a really cool car! So he went to the rental car service and asked to see their sports cars. The man at the counter explained that all of their sports cars had already been booked for the summer... and every other car had been booked for that matter. All they had left were ostriches. "OSTRICHES?" Mr. C exclaimed! "You want me to travel around the state of Michigan on an ostrich?" After thinking about it for only a moment, Mr. C thought that sounded like an awesome idea! He signed the paperwork and paid the man for the ostrich. The man explained that while the ostrich is a dependable animal, it can only travel a maximum of 800 miles in a week.
So, Mr. C mapped out his week long vacation. Here was his plan... Okemos → Battle Creek = 63.6 miles Battle Creek → Midland = 141.5 miles Midland → Detroit = 138.0 miles Detroit → Holland = 180.5 miles Holland → Okemos = 99.7 miles Mr. C wanted to be sure that his total miles was not going to be more than 800... or else his ostrich would not make the trip. Mr. C started to add the miles together, but then quickly realized he didn't need an exact total to answer his question. He just needed to figure out if it was going to be less than 800, not what his exact total miles would be. So he decided to estimate the sum. First, he added the hundreds (1+1+1 = 3 hundreds or 300 miles). Then he added the tens (6+4+3+8+9 = 30 tens or 300 miles). When he added these up he got 600 miles which was well below the 800 maximum miles that the ostrich can travel in a week. His plan would work and he was ready to begin his Ostrich road trip! By using estimation as an appropriate tool in this situation, Mr. C was able to correctly and quickly figure out if his plan was going to work. Mr. C could have added the numbers using a paper and pencil algorithm, but this would have taken him longer. By estimating he found a close-but-easier number that was able to correctly answer his question. |
"Snow Day
To Be Exact" |
|
|
|
|
|
|
- Beat the Clock: How fast can you estimate? (Choose Add Tens or Add 100s)
- Ice Ice Maybe: Estimate to help the penguins get to the tropical island. (Choose Emperor Penguins) - Quiz Quest: How many questions can you get right?! - Connect 4: Play against a friend and be the first to get 4 in a row. (Choose addition) |
5.4 estimating products
|
Josh the giraffe loves to be able to quickly guess how many people are in a room, how many cars are in the street, how many boxes are on the shelf, or even how many seagulls are on the beach. Often, when he is trying to solve a puzzle, he doesn't need an exact answer, just an answer that is good enough. Estimation can save Josh time, money, and helps him make fewer mistakes. Let's help Josh practice some estimation with multiplication.
Giraffes can run at a steady 11 mph pace for very long distances. About how many miles can they run in 3 hours?
The average male giraffes is 18 ft tall. If you stacked 30 giraffes on top of one another, about how tall would they be?
|
|
|
- Beat the Clock: How fast can you estimate? (Choose Multiply Tens)
- Ice Ice Maybe: Estimate to help the penguins get to the tropical island. (Choose Adelie Penguins) - Golf: Estimate your way to a hole in one! - Connect 4: Play against a friend and be the first to get 4 in a row. (Choose multiplication) - PacMan: The word's most famous pie-chart is here to help you estimate! |
5.A U.S. TRADITIONAL ALGORITHM for Multiplication
|
|
|
|
- Fill in the Blank: Can you solve each multiplication puzzle following the U.S. Traditional Algorithm?
|
5.5 partial - product MULTIPLICATION - Part 1
The partial-products method for multiplying is a "low-stress" algorithm. This means that many students find it much easier than the common standard multiplication algorithm that your parents probably did when they went to school. One reason why it is easier is because all the multiplication and addition stays below the problem, helping you to stay neat and organized!
|
Since you are adding each calculation, that is, each partial product, it doesn't mater if you start on the left or the right. Whichever way you start, make sure you always start that way to get help practice the routine of the algorithm.
In the example to the right, 7 is multiplied by each part of 538. 7 x 8 = 56 7 x 30 = 210 7 x 500 = 3,500. Then you add all the partial products together. 56 + 210 + 3,500 = 3,766 |
|
|
|
|
|
- Underwater Adventure - Level A = Solve the multiplication puzzles to survive underwater!
- Multiply It: Use the partial product to solve these 1 x 3 digit multiplication puzzles! |
5.6 PARTIAL - PRODUCT MULTIPLICATION - PART 2
The partial-products method for multiplying can become a bit more challenging when we start to multiply larger numbers because we have to make sure to multiply each part and then remember to add each part when we are done. This can become a bit overwhelming, so it is important to take your time, write neatly, and keep your numbers organized!
|
In the example to the right, we are now using the partial-products method to multiply two 2-digit numbers together. When we multiply 61 x 12 you can see there are a few more parts that we have to multiply.
To start lets multiply 2 x 61. 2 x 1 = 2 2 x 60 = 120 Now lets multiply 10 x 61. 10 x 1 = 10 10 x 60 = 600 Lastly, all we have to do is add all the partial products together. 2 + 120 + 10 + 600 = 732 |
|
|
|
|
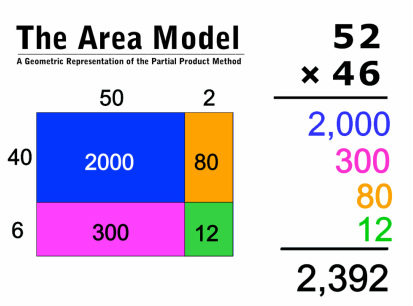
With all the different parts that need to be multiplied when using the Partial-Product Method, many students find it challenging to keep them all organized. It would be helpful if there was a more visual and organized way to make sure we are multiplying each part and not forgetting any. Some students find it helpful to use the Area Model (also known as the Array Model) to help them visualize all the different parts that need to be multiplied.
|
In the example to the right, 52 is multiplied by 46. The Area Model is built off the idea that multiplication can be thought of as a length times a width which gives us the area. Think of a flat. It is 10 cubes long by 10 cubes wide. So it has an area of 100 cubes. We can replicate this thinking when we multiply other numbers. Here, each number is broken up into it's place value and then multiplied against each other. 50 x 40 = 2,000 50 x 6 = 300 2 x 40 = 40 2 x 6 = 12 Lastly, we just add each partial product together. 2,000 + 300 + 80 + 12 = 2,392 |
|
|
|
|
|
- Underwater Adventure - Level B/C = Solve the multiplication puzzles to survive underwater!
- Jeopardy: Can you use the partial-products method to rack up the points? - Make Your Own Worksheet: Build your own practice worksheet. Answer key included! |
5.7 lattice multiplication
The lattice method of multiplication was first printed in an arithmetic book printed in Treviso (Italy) in 1478. Lattice multiplication was first introduced into Europe by Fibonacci (who is also well known for the Fibonacci sequence). He was an Italian who learned how to use the Arabic number system from a Moorish teacher in North Africa. Before the Hindu-Arabic system was used in Europe, multiplication was often done with counters because Roman numerals (I, III, VI, X, C, etc.) were not very useful when doing calculations and very few people knew how to multiply. If you used Everyday Math in 3rd grade, you have hopefully seen this method before. If you have not seen the lattice method before, it can seem a bit confusing at first. But don't worry, you will get the hang of it!
|
|
|
|
|
|
- Quiz Quest: Can you solve these lattice multiplication puzzles?
|
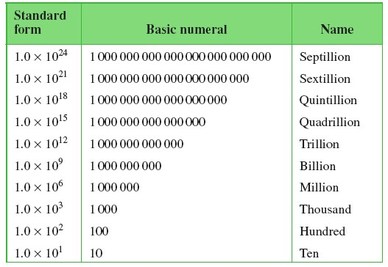
5.8 big numbers
|
HOW BIG IS A BILLION?
|
HOW BIG IS A TRILLION?
|
HOW BIG IS GRAHAM'S NUMBER?
|
|
- How Do You Say That? Type in ANY number and find out how you would say it!
|
5.9 powers of 10
|
Exponents: A small raised number that tells how many times the base is used as a factor.
In this example, the 10 is called the base, and the 2 is called the exponent (sometimes it is also called the index or power). 10² means 10 to the power of 2, or 10 squared. This means that 10 is multiplied by itself 2 times, or we can think of it as 10 x 10 which equals 100! So... 10² = 100 |
|
|
|
Have you ever wondered just how BIG our world is? Travel to the farthest reaches of the known universe and discover just how unimaginably massive our world is. Begin Your Adventure Now! |
|
|
- Review It: Learn more about exponents and the other powers.
- Alien Exponents: Save the world from the alien invasion! - Otter Rush: Be the fastest otter on the race track and win the golden trophy! |
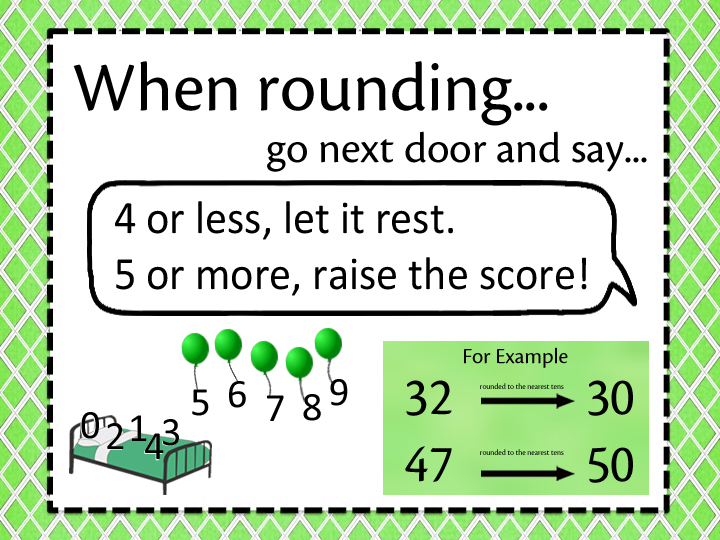
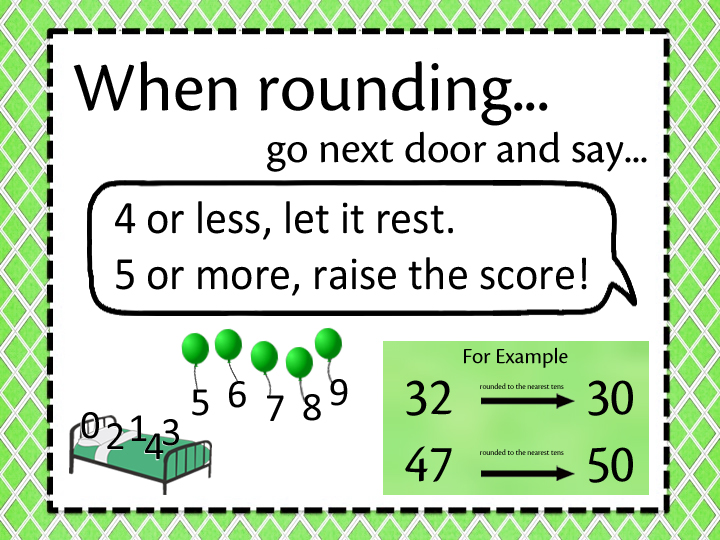
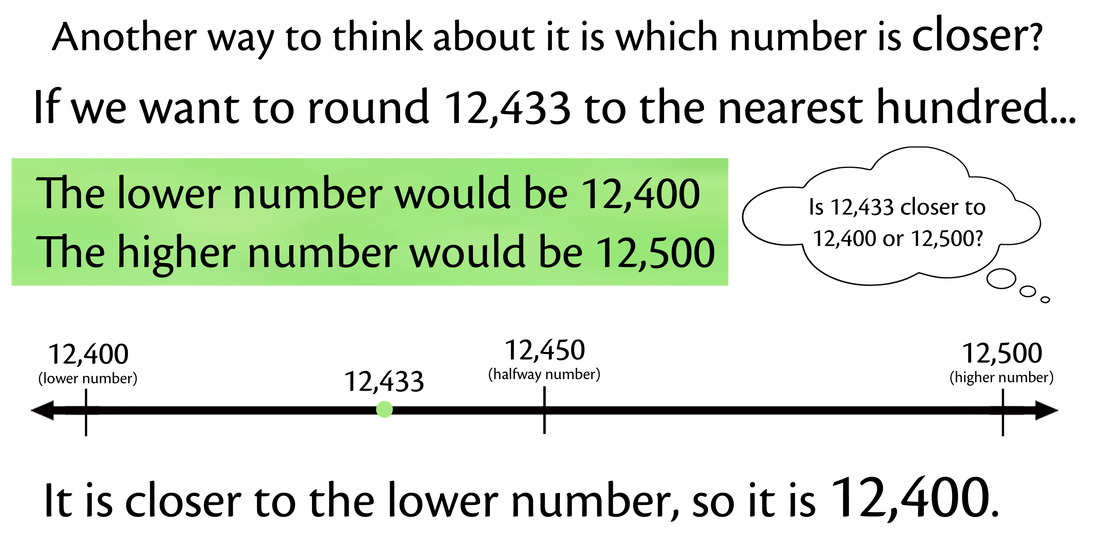
5.10 rounding and reporting large numbers
|
|
|
- Pirate Rounding: Ahoy yee skallywag! Do yous gots what it takes to find the treasure?
- Winter Rounding: Can you make it to level 4 and round numbers bigger than 1,000,000? |
5.11 comparing data
Which mountain is taller?
|
Mt. Everest
29,028 ft
|
Mt. K2
28,250 ft
|
When we compare these two mountain heights, they both look really big. In order to find out which is bigger, we need to look at their exact measurements. Mt. Everest is 29,028 ft tall and Mt. K2 is 28,250 ft tall. If we look at the ten thousands place, they each have a 2. We can't tell which is bigger just by looking at this place value, so we need to go down to the thousands. Mt. Everest = 29,028 Mt. K2 = 28,250
We know that 9,000 is more than 8,000 so... Mt. Everest is taller.
We know that 9,000 is more than 8,000 so... Mt. Everest is taller.
Which river is longer?
|
Huang River
3,395 ft
|
Ob-Irtysh River
3,362 ft
|
Comparing these two rivers, they both look pretty long. To find out which is longer, we need to look at their exact lengths. The Huang River is 3,395 ft long, and the Ob-Irtysh is 3,362 ft long. Let's start with the biggest place value and move down until we see a difference in value. They both have a 3 in the thousands place, and they both have a 3 in the hundreds place. It isn't util we get to the tens place that there is a different number. [Huang River = 3,395 ft / Ob-Irtysh River = 3,362 ft] We know that 90 > 60 so... the Huang River is longer.
|
- Which is BIGGER? Compare different landmarks, people, animals, and planets to see which is bigger.
- Shoot the Fruit: Shoot the fruit and decide which number is bigger. (Choose Level 4, 5, or 6) |
"Show what you know"
are you ready?
Can you find the number with the closest sum?
Can YOU write a number model for the estimate?
Can YOU use the partial-product algorithm to multiply?
Can YOU add or subtract decimals?
Can YOU explain the mistake that Jill made when she solved these problems?
Can YOU use a ruler to measure and record the length of the line segments below to the nearest 1/4 in? What about 1/2 cm?
Can YOU complete the "What's My Rule?" table and state the rule?
- 392 + 239 a. 500 b. 600 c. 700 d. 800
- 983 + 492 a.1,500 b. 1,700 c. 2,000 d. 3,000
Can YOU write a number model for the estimate?
- 203 + 295
- 5,430 + 6,453
Can YOU use the partial-product algorithm to multiply?
- 25 x 4
- 13 x 98
Can YOU add or subtract decimals?
- 9.2 + 8.3
- 4.32 - 1.43
Can YOU explain the mistake that Jill made when she solved these problems?
- 0.2 + 0.35 = 55
- 2.1 + 0.24 = 45
Can YOU use a ruler to measure and record the length of the line segments below to the nearest 1/4 in? What about 1/2 cm?
- __________________________________________________________________ = __________ inches or __________ centimeters
- ___________________________ = __________ inches or __________ centimeters
Can YOU complete the "What's My Rule?" table and state the rule?
Can YOU estimate whether the answer will be in the tens, hundreds, thousands, or more?
Can YOU solve the following questions about this fact: An average of about 500 couples get married in the U.S. every day.
Can YOU explain if George measured correctly?
- 25 x 56 a. 10s b. 100s c. 1,000s d. 10,000s
- 384 x 36 a. 10s b. 100s c. 1,000s d. 10,000s
Can YOU solve the following questions about this fact: An average of about 500 couples get married in the U.S. every day.
- About how many couples get married in one week?
- About how many couples get married in one month?
- Are more or less than 10,000 couples married in a year?
Can YOU explain if George measured correctly?
- George said the line was 6.5 cm long.
